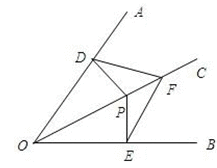
如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA交OA于点D，PE⊥OB交OB于点E，F是OC上另一点，连接DF、EF，求证DF=EF.
答案
∵点P在∠AOB的角平分线OC上′，PE⊥OB，
∴PD=PE，∠DOP=∠EOP，∠PDO=∠PEO=90°，
∴△DPO≌△EPO，
∴∠DPO=∠EPO，
∴∠DPF=∠EPF，
在△DPF和△EPF中，PD=PE，∠DPF=∠EPF，PF=PF
∴△DPF≌△EPF
∴DF=EF．
知识点：三角形的外角性质 全等三角形的性质 全等三角形的判定 角平分线的性质
根据角平分线的性质，得PD=PE，根据三角形的外角的性质，得∠DPF=∠EPF，再根据SAS证明△DPF≌△EPF，则DF=EF．
对角平分线的性质掌握不牢
WORD格式（
