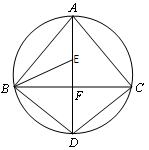
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B、E、C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
答案
(1)AD⊥BC,由垂径定理得,BD=CD
(2)因为BE是∠ABC角平分线,所以∠ABE=∠FBE,由垂径定理=
,等弧所对的圆周角相等,所以∠BAD=∠DBC,∠DBE=∠DBF+∠FBE,∠DEB=∠ABE+∠BAE,所以有∠DBE=∠BED,所以BD=ED,又BD=CD,所以BD=ED=CD,B、E、C三点都在以点D为圆心,BD为半径的圆上。
(1)AD⊥BC,由垂径定理得,BD=CD
(2)因为BE是∠ABC角平分线,所以∠ABE=∠FBE,由垂径定理=
,等弧所对的圆周角相等,所以∠BAD=∠DBC,∠DBE=∠DBF+∠FBE,∠DEB=∠ABE+∠BAE,所以有∠DBE=∠BED,所以BD=ED,又BD=CD,所以BD=ED=CD,B、E、C三点都在以点D为圆心,BD为半径的圆上。
略








