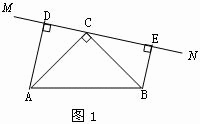
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证: ①△ACD≌△CEB;②DE=AD+BE;
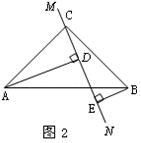
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
答案
(1)∵AD⊥MN,BE⊥MN
∴∠ADC=∠CEB=90°
∴∠CAD+∠ACD=90°
又∠BCE+∠ACD=90°
∴∠CAD=∠BCE
又∵AC=BC,∠ADC=∠CEB
∴△ACD≌△CBE
∴AD=CE,CD=BE
∴DE=AD+BE
(2)①成立、②不成立,理由如下:
∵AD⊥MN,BE⊥MN
∴∠ADC=∠CEB=90°
∴∠CAD+∠ACD=90°
又∠BCE+∠ACD=90°
∴∠CAD=∠BCE
又∵AC=BC,∠ADC=∠CEB
∴△ACD≌△CBE
∴AD=CE>DE
∴①成立、②不成立
知识点:全等三角形的判定与性质 直角三角形的性质
利用全等三角形的判定方法证明三角形全等,本题中可以利用同角的余角相等来导角
对三角形全等方面的知识不熟悉









