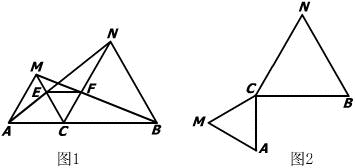
如图1,点C为线段AB上一点,△ACM, △CBN是等边三角形,直线AN,BM分别交两三角形于点E、F.连结EF.
(1)求证:AN=BM;
(2)求证: △CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明);
答案
(1)∵△ACM, △CBN是等边三角形
∴AC=CM,CN=CB,ACM=
BCN=60°
∴ACN=
MCB=120°
∴△ACN≌△MCB
∴AN=MB
(2)由△ACN≌△MCB,得∠CMB=∠CAN
在△CMF和△CAE中
∴△CMF≌△CAE
∴CF=CE
又∵∠ECF=60°
∴△CEF为等边三角形(有一个角为60°的等腰三角形为等边三角形)
(3)连接BM交AC于点F,连接AN交BC于点E
此时第(1)小题的结论仍然成立,第(2)小题的结论不成立
知识点:全等三角形的判定与性质 等边三角形的性质
(1)证明两条线段相等,而且这两条线段没有公共端点,所以我们想到用证明三角形全等的方法,△ACN含有AN,△MCB含有BM,从而我们着手证明这两个三角形全等
(2)在△CEF中,观察到∠ECF=60°,只需要证明出△CEF为等腰三角形即可证明出结论,又是证明两条线段相等,我们想到用全等,观察到CF在△CMF里,CE在△CEA中,并且这两个三角形看着像全等,所以我们着手证明这两个三角形全等,并且不要忘记在做第二问的时候,要看看第一问我们证明的结论有没有用
(3)在补出符合要求的图形后,根据前两问的思路很容易得出第三问的答案。
这道题的难点在于:第二问看不出要证明哪两条边相等,即找不出所在的哪两个三角形是全等的








