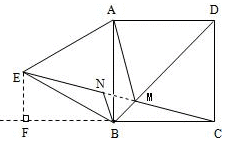
如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.
（1）求证：△AMB≌△ENB；
（2）①当M点在何处时，AM＋CM的值最小；
②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；
（3）当AM＋BM＋CM的最小值为 $\sqrt{3}+1$ 时，求正方形的边长.

答案

解：（1）∵△ABE是等边三角形，∴BA=BE，∠ABE=60°．∵∠MBN=60°，∴∠MBN-∠ABN=∠ABE-∠ABN．即∠ABM=∠ENB．又∵MB=NB，∴△AMB≌△ENB（SAS）．
（2）①当M点落在BD的中点时，AM+CM的值最小．②如图，连接CE，当M点位于BD与CE的交点处时，AM+BM+CM的值最小．
理由如下：连接MN，由（1）知，△AMB≌△ENB，∴AM=EN，∵∠MBN=60°，MB=NB，∴△BMN是等边三角形．∴BM=MN．∴AM+BM+CM=EN+MN+CM．根据“两点之间线段最短”，得EN+MN+CM=EC最短，∴当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长．
（3）过E点作EF⊥BC交CB的延长线于F，∴∠EBF=90°-60°=30°．设正方形的边长为x，则BF= $\frac{\sqrt{3}}{2}x$ ，EF= $formdata=\fs2+\frac{x}{2}$ ．在Rt△EFC中，∵EF²+FC²=EC²，∴（ $formdata=\fs2+\frac{x}{2}$ ）²+（ $\frac{\sqrt{3}}{2}x$ +x）²= $formdata=\fs2+{\left({\sqrt{3}+1}\right)^2}$ ．解得，x= $formdata=\fs2+\sqrt{2}$ （舍去负值）．∴正方形的边长为 $formdata=\fs2+\sqrt{2}$ ．

知识点：正方形的性质轴对称-最短路线问题

（1）由题意得MB=NB，∠ABN=15°，所以∠EBN=45°，容易证出△AMB≌△ENB；
（2）①根据“两点之间线段最短”，可得，当M点落在BD的中点时，AM+CM的值最小；
②根据“两点之间线段最短”，当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长（如图）；
（3）作辅助线，过E点作EF⊥BC交CB的延长线于F，由题意求出∠EBF=30°，设正方形的边长为x，在Rt△EFC中，根据勾股定理求得正方形的边长为 $formdata=\fs2+\sqrt{2}$ ．
具体解题过程如下：
解：（1）∵△ABE是等边三角形，∴BA=BE，∠ABE=60°．∵∠MBN=60°，∴∠MBN-∠ABN=∠ABE-∠ABN．即∠ABM=∠ENB．又∵MB=NB，∴△AMB≌△ENB（SAS）．
（2）①当M点落在BD的中点时，AM+CM的值最小．②如图，连接CE，当M点位于BD与CE的交点处时，AM+BM+CM的值最小．
理由如下：连接MN，由（1）知，△AMB≌△ENB，∴AM=EN，∵∠MBN=60°，MB=NB，∴△BMN是等边三角形．∴BM=MN．∴AM+BM+CM=EN+MN+CM．根据“两点之间线段最短”，得EN+MN+CM=EC最短，∴当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长．
（3）过E点作EF⊥BC交CB的延长线于F，∴∠EBF=90°-60°=30°．设正方形的边长为x，则BF= $\frac{\sqrt{3}}{2}x$ ，EF= $formdata=\fs2+\frac{x}{2}$ ．在Rt△EFC中，∵EF²+FC²=EC²，∴（ $formdata=\fs2+\frac{x}{2}$ ）²+（ $\frac{\sqrt{3}}{2}x$ +x）²= $formdata=\fs2+{\left({\sqrt{3}+1}\right)^2}$ ．解得，x= $formdata=\fs2+\sqrt{2}$ （舍去负值）．∴正方形的边长为 $formdata=\fs2+\sqrt{2}$ ．

最短问题掌握不牢

下载次数：3

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>