在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A₁B₁C₁.
（1）如图1，当AB∥CB₁时，设A₁B₁与CB相交于点D.
证明：△A₁CD是等边三角形；
（2）如图2，连接A₁A、B₁B，设△ACA₁和△BCB₁的面积分别为和，
求证：： =1:3
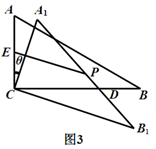
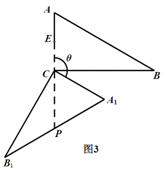
（3）如图3，设AC中点为E，A₁B₁中点为P，AC=a，连接EP，当θ=_____°时，EP长度最大，最大值为_________.

答案

（1）证明：如图，∵AB∥CB₁，∴∠BCB₁=∠B=∠B₁=30°，∴∠A₁CD=90°-∠BCB₁=60°，∠A₁DC=∠BCB₁+∠B₁=60°，∴△A₁CD是等边三角形；
（2）证明：由旋转的性质可知，∠ACA₁=∠BCB₁，AC=CA₁，BC=CB₁，∴△ACA₁∽△BCB₁，∴： =AC²：BC²=1²：²=1：3；
（3）如图3，连接CP，当△ABC旋转到E、C、P三点共线时，EP最长，此时θ=∠ACA₁=120°，EP=EC+CP= a+a= a．故答案为：120，a．

知识点：轴对称-最短路线问题  旋转的性质  

解题思路：（1）当AB∥CB₁时，∠BCB₁=∠B=∠B₁=30°，则∠A₁CD=90°-∠BCB₁=60°，∠A₁DC=∠BCB₁+∠B₁=60°，可证：△A₁CD是等边三角形；
（2）由旋转的性质可证△ACA₁和△BCB₁，利用相似三角形的面积比等于相似比的平方求解；
（3）连接CP，当E、C、P三点共线时，EP最长，根据图形求出此时的旋转角及EP的长．
具体过程如下：
（1）证明：如图，∵AB∥CB₁，∴∠BCB₁=∠B=∠B₁=30°，∴∠A₁CD=90°-∠BCB₁=60°，∠A₁DC=∠BCB₁+∠B₁=60°，∴△A₁CD是等边三角形；
（2）证明：由旋转的性质可知，∠ACA₁=∠BCB₁，AC=CA₁，BC=CB₁，∴△ACA₁∽△BCB₁，∴： =AC²：BC²=1²：²=1：3；
（3）如图3，连接CP，当△ABC旋转到E、C、P三点共线时，EP最长，此时θ=∠ACA₁=120°，EP=EC+CP= a+a= a．故答案为：120，a．

易错在第三问，缺乏思路。

下载次数：8

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>