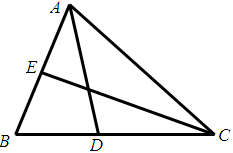
如图，△ABC中，∠ABC=60°，AD、CE分别平分∠BAC，∠ACB，判断AC的长与AE+CD的大小关系并证明.

答案

判断：AC=AE+CD
证明：令AD与CE的交点为G，在AC上截取AF=AE，

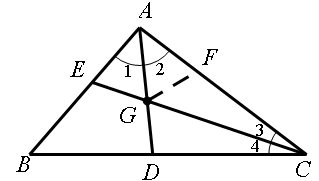
在△AEG和△AFG中
∴△AEG≌△AFG（SAS），∴∠AGE=∠AGF；∵∠ABC=60°，∴∠BAC+∠BCA=120°，又AD、CE分别为∠BAC和∠BCA的角平分线，所以∠2+∠3=60°，从而∠AGE=60°；于是∠AGF=∠AGE=60°，∠CGD=∠AGE=60°，从而∠CGF=60°；在△CGF和△CGD中∴△CGF≌△CGD，∴CD=CF，从而AC=AF+CF=AE+CD。

知识点：三角形  三角形的外角性质  全等三角形的性质  全等三角形的判定  

看到两段不相干的线段与另一条线段的关系的题目一定要想到分解较长线段，分别证明相等。

未将全部条件找全就使两个三角形全等

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>