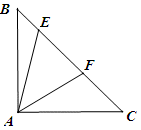
如图，在Rt△ABC中，∠BAC=90°，AB=AC，E、F分别是BC上两点，若∠EAF=45°，试推断BE、CF、EF之间的数量关系，并说明理由.

答案

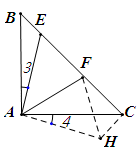
EF²=CF²+BE²
绕点A顺时针旋转△BEA到CHA，连接FH，则CH=BE，∠ACH=∠B，∠4=∠3.
∵ ∠BAC=90°，∠B+∠FCA=90°，
∴ ∠EAH=90°，∠ACH+∠FCA=∠FCH=90°
又∠EAF=45°，∴ ∠FAH=45°
在△EFA与△HFA中
  AE=AH
  ∠EAF=∠HAF=45°
  AF=AF
∴ △EAF≌△HFA（SAS）
∴ HF=EF
在Rt△FCH中，CF²+CH²=HF²
∴  EF²=CF²+BE²

 

知识点：勾股定理  旋转的性质  

通过旋转构造一个直角三角形，由勾股定理得到一个等式，然后利用等量关系代换，得到我们所要的结论。

我们要找三边之间的关系，只有放在一个三角形里面才能判断，所以通过旋转，把已知的三边转化到一个三角形中。

下载次数：5

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>