如图，在Rt△ABC中，∠A=90°，D为斜边BC中点，DE⊥DF，求证：EF²=BE²+CF².

答案

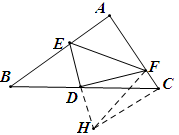
做∠DCH=∠B，并使CH=BE，连接DH。则△DCH≌△DBE（SAS）
则ED=HD
∵ ∠B+∠ACB=90°
∴ ∠DCH+∠ACB=90°
在直角三角形FCH中，HF²=CH²+CF²=BE²+CF²
又∵   ∠EDF=90°，∴∠BDE+∠FDC=90°
∵∠CDH=∠BDE，∴∠FDH=90°，∴E、D、H在同一直线上。
∵ED=DH，DF⊥ED
∴ EF=HF
∴ EF²=BE²+CF²

知识点：勾股定理  旋转的性质  

不会通过旋转建立条件与结论之间的关系

大部分学生不会把三边EF、BE、CF转化到一个直角三角形中。

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>