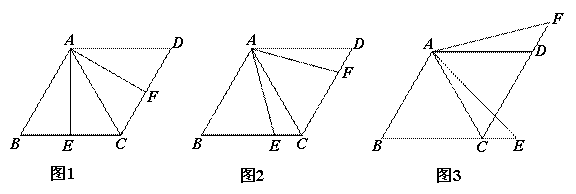
已知菱形ABCD中,∠BAD=120°,过点A分别作AE⊥BC于E,AF⊥CD于F,且∠EAF=60°,证明:BE+DF=AB;当∠EAF绕着点A逆时针方向旋转到∠EAF的两边与菱形的两边BC、CD(或两边BC、CD的延长线)相交,但不垂直时(如图2、图3),上述结论是否还成立.如果成立,请给予证明;如果不成立,写出线段BE、DF、AB三者之间的数量关系,并证明.
答案
证明:(1)如图,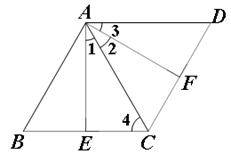
在菱形ABCD中,AB=BC=CD=DA,∠BAD+∠B=180°
∵∠BAD=120°
∴∠B=60°
∴△ABC是等边三角形
∴∠4=60°
同理△ACD是等边三角形
∴AC=AD,∠CAD=∠D=60°
∴∠4=∠D
∵∠1+∠2=60°,∠2+∠3=60°
∴∠1=∠3
∴△AEC≌△AFD
∴EC=FD
∵BE+EC=BC=AB
∴BE+FD=AB
(2)如图2,依然成立.
证明过程仿照例(1),
可证△AEC≌△AFD,
最终BE+FD=AB
(3)如图3,此时BE=AB+DF
证明过程仿照例(2),
可证△AEC≌△AFD
∴CE=DF
∵BE=BC+CE
∴BE=AB+DF
知识点:菱形大角夹半角
略
略








