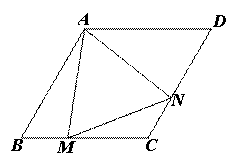
如图,菱形ABCD中,∠BAD=120°,点M为BC上一点,点N为CD上一点,若△AMN有一个角等于60°,试判断△AMN的形状,并说明理由.
答案
解:△AMN是等边三角形,理由如下:
①∠MAN=60°,如图,连接AC
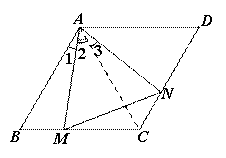
∵菱形ABCD中,∠BAD=120°
∴∠B=∠ACD=∠BAC=60°,AB=AC
即∠1+∠2=60°
∵∠MAN=60°
∴∠2+∠3=60°
∴∠1=∠3
∴△ABM≌△ACN
∴AM=AN
∵∠MAN=60°
∴△AMN是等边三角形
②∠AMN=60°
如图,连接AC交MN于点F,过点M作ME∥AC交AB于点E
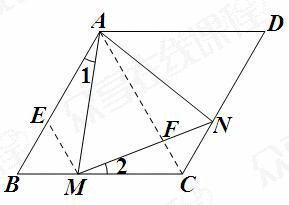
∵菱形ABCD中,∠BAD=120°
∴△ABC与△ACD为等边三角形,∠BCD=120°
∴AB=BC
∴∠B=60°
∴△BME为等边三角形
∴EM=BM=BE,∠BEM=60°
∴∠AEM=120°
∴∠AEM=∠BCD
∴AB-BE=BC-BM
即AE=MC
∵∠AMC为△ABM的一个外角
∴∠AMC=∠B+∠1
∵∠AMC=∠AMN+∠2
∵∠AMN=∠B=60°
∴∠1=∠2
∴△AEM≌△MCN
∴AM=MN
∵∠AMN=60°
∴△AMN是等边三角形
③∠ANM=60°时类比∠AMN=60°可证:△AMN是等边三角形
综上:若△AMN有一个角等于60°,△AMN为等边三角形
知识点:菱形大角夹半角
略
略








