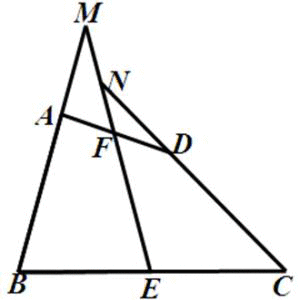
在四边形ABCD中，AB＝CD，BC、AD的中点分别是E、F，BA、EF的延长线交于点M，CD、EF交于点N；求证：∠BME＝∠CNE．
答案
连接BD，作FH∥BA交BD于H，连接HE．如下图：
∵F是DA的中点，且FH∥BA，
∴FH= BA，H是BD的中点，又因为E是BC的中点
∴HE∥CD，且HE= CD．
∵BA=CD，
∴FH=HE，三角形HFE为等腰三角形，即∠HFE=∠HEF．
∵FH∥BM，∴∠HFE=∠BME
∵EH∥CN，∴∠HEF=∠CNE
∴∠BME=∠CNE．
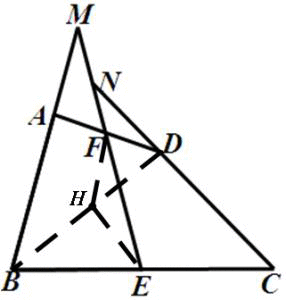
连接BD，取BD的中点H，连接HE、HF，根据三角形中位线定理，证明HE=HF，从而∠HFE=∠HEF，再利用平行线性质，可证得∠BME=∠CNE
考查平行线对角相等，同位角相等，中位线平行且等于对应边，等腰三角形底角相等．
WORD格式（
