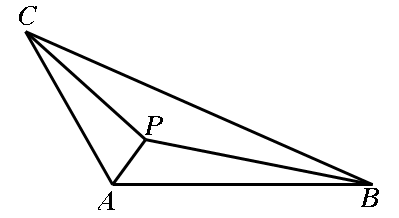
如图所示，在△ABC中，∠BAC=120°，P是△ABC内部一点，试比较PA+PB+PC与AB+AC的大小关系.
答案
延长BA到D使AD=AC，连接DC，作∠DCE=∠ACP，且CE=CP，连接DE、EP
易证△ADC是等边三角形，△DCE≌△ACP
∴AC=CD=AD，
∴∠ECP=∠DCA-∠DCE+∠ACP=60°
又CE=CP，∴△CEP是等边三角形，
∴CP=EP，
可得：PA+PB+PC=DE+PE+PB＞DA+AB，
∴PA+PB+PC＞AC+AB．
知识点：三角形三边关系 全等三角形的判定与性质 等边三角形的判定与性质
作辅助线延长BA到D使AD=AC，连接DC，易证明△ADC是等边三角形，△CEP也是等边三角形，由此可得．
不会把边都转到一个三角形中
WORD格式（
