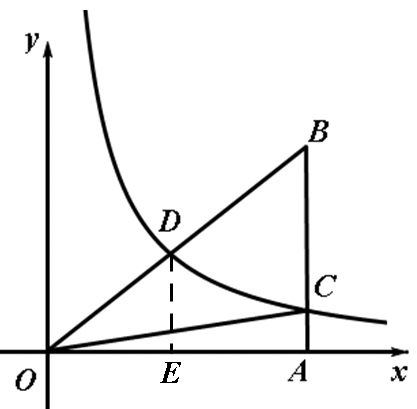
（2010荆州）已知：关于x的一元二次方程x²+(2k-1)x+k²=0的两根x₁、x₂满足x₁²-x₂²=0，双曲线经过Rt△OAB斜边OB的中点D，与直角边AB交于点C，求S_△OBC
.

答案

解：∵x²+（2k-1）x+k²=0有两根，
∴△=（2k-1）²-4k²≥0，
即 k≤．
由x₁²-x₂²=0得：（x₁-x₂）（x₁+x₂）=0．
当x₁+x₂=0时，-（2k-1）=0，解得 k=，不合题意，舍去；
当x₁-x₂=0时，x₁=x₂，△=（2k-1）²-4k²=0，
解得： k=符合题意．
∴双曲线的解析式为： y=．
过D作DE⊥OA于E，则 S_△ODE=S_△OCA
∵DE⊥OA，BA⊥OA，
∴DE∥AB，∴△ODE∽△OBA，
∴ ，∴ S_△OBA=
∴ S_△OBC=S_△OBA-S_△OCA

知识点：反比例函数综合题  

首先由一元二次方程根的判别式得出k的取值范围，然后由x₁²-x₂²=0得出x₁-x₂=0或x₁+x₂=0，再运用一元二次方程根与系数的关系求出k的值，由k的几何意义，可知S_△OCA= |k|．如果过D作DE⊥OA于E，则S△ODE= |k|．易证△ODE∽△OBA，根据相似三角形的面积比等于相似比的平方，得出S_△OBA，最后由S_△OBC=S_△OBA-S_△OCA，得出结果．

没有看出反比例函数与面积之间的关系。

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>