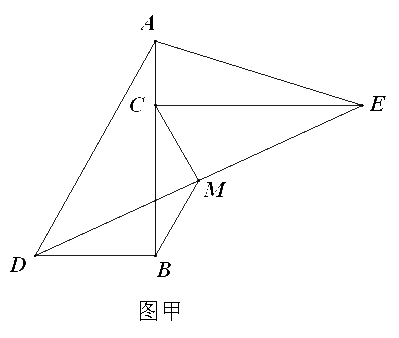
已知：△ABD和△ACE都是直角三角形，且∠ABD=∠ACE=90°。如图甲，连结DE，设M为DE的中点。
（1）求证：MB=MC；
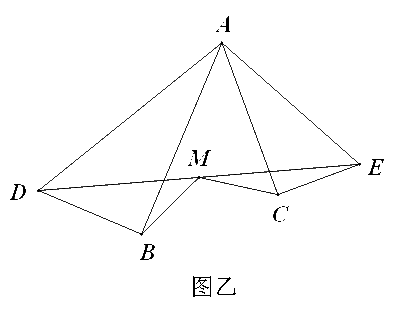
（2）设∠BAD=∠CAE，固定△ABD，让Rt△ACE绕顶点A在平面内旋转到图乙的位置，试问：MB=MC是否还能成立？并证明其结论。

答案

（1）分别取AE，AD的中点P和Q

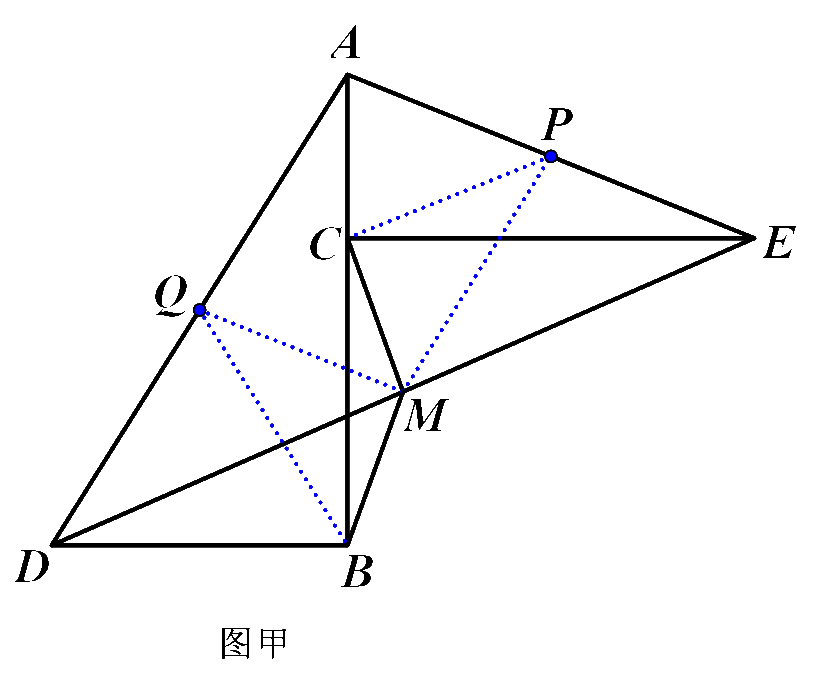
（1）在Rt△ACE中，P为斜边AE的中点

∴CP=AE，
同理在Rt△ABD中，BQ=AD
∵P为AE的中点，M为DE的中点
∴PM为△ADE的中位线
∴PM∥AD，且PM=AD
同理QM∥AE，且QM=AE
∴BQ=PM，CP=QM
∠BQM=∠DQM-∠DQB=∠DQM-2∠DAB
∠MPC=∠APM-∠APC
∴∠BQM-∠MPC=（∠DQM-2∠DAB）-（∠APM-∠APC）
∵QM∥AE，∴∠DQM=∠DAE
∵PM∥AD，∴∠APM=180°-∠DAE
∴∠BQM-∠MPC=（∠DQM-2∠DAB）-（∠APM-∠APC）
               =∠DAE-2∠DAB-（180°-∠DAE）+∠APC
               =2∠DAE-2∠DAB-180°+∠APC
               =2∠CAP+∠APC-180°
               =0
即∠BQM=∠MPC
在△BMQ和△MCP中
BQ=MP，∠BQM=∠MPC，MQ=CP
∴△BMQ≌△MCP
∴BM=MC
     （2）第二问可以类比第一问的思路来做请同学们独立完成。

知识点：直角三角形斜边上的中线  三角形中位线定理  

<<上一题   下一题>>