如图，梯形ABCD中，AD∥BC，CE⊥AB，△BDC为等腰直角三角形，CE与BD交于点F，连接AF，G为BC中点，连接DG交CF于点M.证明：（1）CM=AB；（2）CF=AB+AF.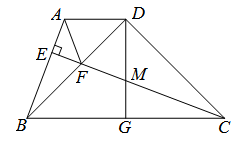
答案
证明：（1）∵△BDC为等腰直角三角形，CE与BD交于F
∴BD⊥CD，BE⊥CE
∴∠EBF+∠EFB=90°，∠DFC+∠DCF=90°
∵∠EFB=∠DFC
∴∠EBF=∠DCF又
∵G为BC中点，AD∥BC
∴∠ADB=∠DBG=∠MDC=45°
在△ABD与△MCD中
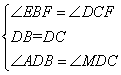
∴△ABD≌△MCD
∴CM=AB
（2）∵△ABD≌△MCD
∴AD=MD又
∵G为BC中点，AD∥BC
∴∠ADB=∠DBG=∠MDB=45°
在△AFD与△MFD中
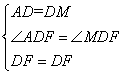
∴△AFD≌△MFD
∴AF=MF
∴CF=CM+MF=AB+AF
∴CF=AB+AF
知识点：梯形
略
略
WORD格式（
