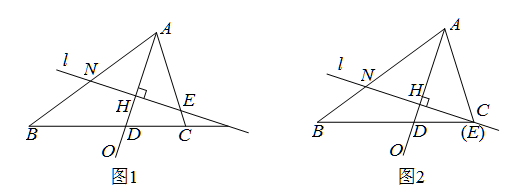如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为线段AD上一动点,过点H作直线l⊥AO于点H,分别交直线AB,AC于点N,E.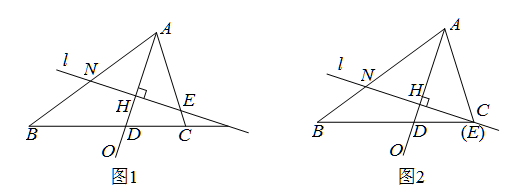
(1)当直线l经过点C时(如图2),证明:BN=CD;(2)猜想BN,CE,CD之间的等量关系并证明你的猜想.
答案
(1)证明:连接ND.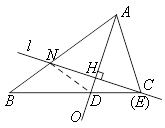
∵AO平分∠BAC,
∴∠NAD=∠DAC,
∵直线l⊥AO于H,
∴∠NHA=∠CHA=90°,
∴∠ANH=∠ACH,
∴AN=AC,
∴NH=CH,
∴AH是线段NC的中垂线,
∴DN=DC,
∴∠HND=∠HCD.
∴∠AND=∠ACB,
∵∠AND=∠B+∠NDB,∠ACB=2∠B,
∴∠B=∠NDB,
∴BN=DN.
∴BN=DC;
(2)BN、CE、CD之间的等量关系:①当点E在线段AC上时,BN=CD+CE;②当点E在AC的延长线上时,CD =BN+CE.
理由如下:①当点E在线段AC上时.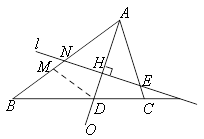
在AB上取一点M,使AM=AC,连接DM.
∵AO平分∠BAC,
∴∠NAD=∠DAC,
∵AM=AC,AD=AD,
∴△AMD≌△ACD
∴∠AMD=∠ACD,MD=CD
∵∠AMD=∠B+∠MDB,∠ACB=2∠B,
∴∠B=∠MDB,
∴BM=MD,
∴BM=CD,
∵直线l⊥AO于H,
∴∠NHA=∠CHA=90°,
∴∠ANH=∠AEH,
∴AN=AE,
∵AM=AC,
∴MN=CE,
∴BN=BM+MN=CD+CE,即BN=CD+CE;
②当点E在AC的延长线上时.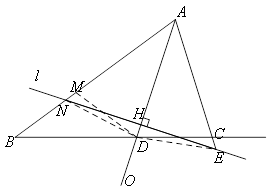
在AB上取一点M,使AM=AC,连接DM,DE,DN.
∵AO平分∠BAC,
∴∠NAD=∠DAC,
∵AM=AC,AD=AD,
∴△AMD≌△ACD
∴∠AMD=∠ACD,MD=CD
∵∠AMD=∠B+∠MDB,∠ACB=2∠B,
∴∠B=∠MDB,
∴BM=MD,
∴BM=CD,
∵直线l⊥AO于H,
∴∠NHA=∠CHA=90°,
∴∠ANH=∠AEH,
∴AN=AE,
∵AM=AC,
∴MN=CE,
∴CD=BM=BN+MN=BN+CE,即CD =BN+CE.
知识点:线段垂直平分线的性质 三线合一
略
略