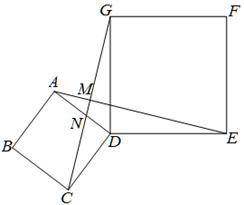
如图，在正方形ABCD，DEFG中，AD=CD，DE=DG，∠EDG＝∠ADC=90°，连接CG交AD于点N，连接AE交CG于点Ｍ．
（1）求证：AE=CG；
（2）观察图形，猜想AE与CG之间的位置关系，并证明你的猜想．

答案

证明：如图，
（1）∵∠EDG＝∠ADC
∴∠EDG+∠ADG=∠ADC+∠ADG
即∠ADE＝∠CDG
在△ADE和△CDG中

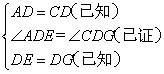
∴△ADE≌△CDG（SAS）
∴AE=CG
(2)AE⊥CG
∵∠ADC=90°
∴∠GCD+∠CND=90°
∵△ADE≌△CDG
∴∠EAD＝∠GCD
∵∠ANG＝∠CND
∴∠EAD+∠ANG=90°
∴∠AMC=90°
即：AE⊥CG

知识点：三角形全等  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>