已知：如图，在△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC，交CF的延长线于D．（1）求证：AE=CD；（2）若AC=12cm，求BD的长．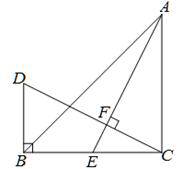
答案
证明：如图，
（1）∵CF⊥AE
∴∠AFC=90°
∴∠ACF+∠FAC=90°
∵∠ACB=∠ACF+∠BCD=90°
∴∠FAC=∠BCD
∵BD⊥BC
∴ ∠DBC=90°
∴∠ACB=∠DBC
在△ECA和△DBC中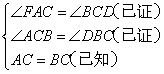
∴△ECA≌△DBC（AAS）
∴AE=CD
（2）∵△ECA≌△DBC
∴AC=BC，CE=BD
∵AE是BC边上的中线
∴CE＝
BC
∴BD=AC
∵ AC=12
∴ BD=6
即：BD的长为6cm.
知识点：三角形全等
略
略
WORD格式（
