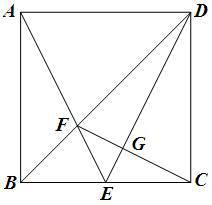
如图,四边形ABCD为正方形,∠ABE=∠DCE=90°,AB=BC=CD=AD,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,∠ABF=∠CBF,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.

解:垂直.理由如下:
在△ABF与△CBF中
                 
∴               
∴∠BAF=∠BCF
在Rt△ABE和Rt△DCE中
                      
∴                   
∴∠BAE=∠CDE
∴∠BCF=∠CDE
∵∠CDE+∠DEC=90°
∴∠BCF+∠DEC=90°
∴DE⊥CF
①,②,③,④,⑤Rt△ABE≌Rt△DCE(HL),⑥△ABE≌△DCE(SAS),⑦△ABF≌△CBF(SAS),⑧△ABF≌△CBF(SSS),
以上空缺处依次填写正确的顺序为()

• A.①⑦④⑥
• B.②⑧③⑤
• C.①⑦③⑤
• D.②⑧④⑥

答案

正确答案：C

知识点：全等三角形证明过程训练,全等三角形的判定和性质  

略

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>