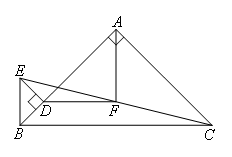
已知：如图，△ABC与△BDE均为等腰直角三角形，BA⊥AC，ED⊥BD，垂足分别为点A，点D，连接EC，F为EC中点，连接AF，DF，请猜测AF，DF的数量关系和位置关系，并说明理由．
   

答案

解：AF⊥DF，AF=DF，理由如下：
      延长DF交AC于点P.
     
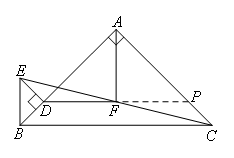
      ∵BA⊥AC，ED⊥BD
      ∴∠BAC=∠EDA=90°
      ∴DE∥AC
      ∴∠DEC=∠ECA
      ∵F为EC中点
      ∴EF=FC
      在△EDF和△CPF中
       
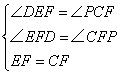
      ∴△EDF≌△CPF（AAS）
      ∴DE=CP，DF=PF
      ∵△ABC与△BDE均为等腰直角三角形
      ∴AB=AC，DE=BD
      ∴AB-BD=AB-DE
                 =AC-CP
        即AD=AP
      在△DAF和△PAF中
       
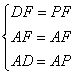
      ∴△DAF≌△PAF（SSS）
      ∴∠DFA=∠PFA=90°，∠DAF=∠PAF=45°
      ∴AF⊥DF，AF=DF

知识点：三角形全等之倍长中线  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>