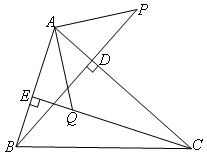
已知：如图，BD，CE是△ABC的高，点P在BD的延长线上，BP=AC，点Q在CE上，CQ=AB．
判断线段AP和AQ的位置关系和数量关系，并证明．

答案

解：AP⊥AQ，AP=AQ，理由如下：
    ∵BD，CE是△ABC的高
    ∴∠ADB=∠ADP=∠AEC=90°
    ∴∠P＋∠CAP=90°
      ∠BAC＋∠ACE=90°
      ∠BAC＋∠ABD=90°
    ∴∠ACE=∠ABD
    在△APB和△QAC中
   
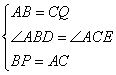
    ∴△APB≌△QAC（SAS）
    ∴AP=AQ（全等三角形对应边相等）
      ∠P=∠QAC（全等三角形对应角相等）
    ∴∠QAP=∠QAC＋∠CAP=90°
    ∴AP⊥AQ

知识点：三角形全等的判定及性质  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>