如图，等边△ABC中，在顶点A、C处各有一只蚂蚁，他们同时出发，分别以1cm/s的速度由A向B和由C向A爬行，经过t秒后，他们分别到达D，E处．请问两只蚂蚁在爬行过程中：
（1）BE与CD有何数量关系，为什么？
（2）BE与CD所成的∠BFC的大小是否发生变化？若有变化，请说明理由，若没有变化，求出∠BFC．
答案
解：如图，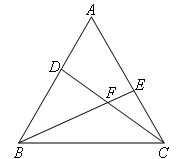
（1）BE=CD，理由如下：
由题意得AD=t，CE=t
∴AD=CE
∵△ABC是等边三角形
∴∠A=∠ACB=∠ABC=60°，AC=CB
在△DAC和△ECB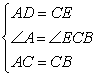
∴△DAC≌△ECB（SAS）
∴BE=CD
（2）∠BFC=120°，没有发生变化，理由如下：
如图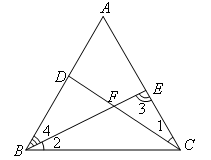
∵△DAC≌△ECB
∴∠1=∠2
∵∠2+∠4=60°
∴∠1+∠4=60°
∵∠3是△ABE的一个外角
∴∠3=∠A+∠4
∵∠BFC是△CFE的一个外角
∴∠BFC=∠1+∠3
=∠1+∠4+∠A
=60°+60°
=120°
知识点：动点问题
略
略
WORD格式（
