已知：如图，正方形ABCD的边长为4，动点P从点A出发沿AB-BC-CD方向以每秒2个单位的速度匀速运动，到达点D时停止运动．连接AP，DP．设点P运动时间为x秒，求当x为何值时，能使△ADP的面积为6．
答案
解：如图，在正方形ABCD中
AB=BC=CD=DA=4
①当点P在AB上运动时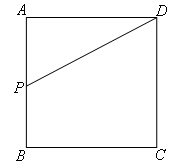
由题意得：AP=2x
若使
，则需
×AD×AP=6
∴·4·2x=6，x=
即当x=时，
②当点P在BC上运动时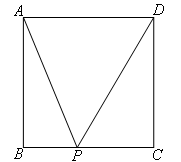
×AD×AB=×4×4=8
故不存在x使．
③当点P在CD上运动时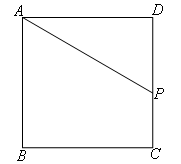
由题意得：DP=4+4+4-2x =12-2x
若使，则需×AD×DP=6
∴·4·(12-2x)=6，x=
即当x=时，
综上所述，当x=或x=时，．
知识点：动点问题
略
略
WORD格式（
