已知:如图,在Rt△ABC中,AB=BC,∠ABC=90°.一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于点E、F,图1、图2是旋转三角板所得图形的两种情况.
(2)若点E和点F分别在AB和BC边的延长线上时,如图2,OE=OF还成立吗?若成立,请给出证明,若不成立,请说明理由.

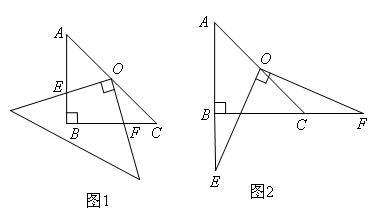
解题思路:(2)类比(1)的思路,添加的辅助线是           ,因为AB=BC,∠ABC=90°,所以△ABC是一个等腰直角三角形;根据点O是AC的中点,得到BO⊥AC,进而得到△BOC是等腰直角三角形,所以OB=OC,∠ACB=∠CBO=45°,又因为∠EOF=90°,根据           ,可以得到           ,又因为∠OBE=∠OCF=135°,根据全等三角形判定定理           ,可以得到           ,根据全等三角形的性质可以得到OE=OF.
①连接OB,②连接OB,使OB⊥AC,③∠BOE=∠FOC,④∠AOE=∠FCO,⑤同角的补角相等,⑥同角的余角相等,⑦△AOE≌△COF,⑧△BOE≌△COF,⑨AAS,⑩ASA,
以上横线处,依次所填正确的是(    )

• A.②⑥③⑩⑧
• B.②⑤④⑩⑦
  
• C.①⑥④⑧⑨
• D.①⑥③⑩⑧
  

答案

正确答案：D

知识点：三角形全等之类比探究  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>