方法感悟:(1)已知:如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:EF=DE+BF.
解题思路:
延长CB到G,使BG=DE,连接AG;在正方形ABCD中,AB=AD,∠ABG=∠D=∠BAD=90°;根据全等三角形判定定理可以得到△ABG≌△ADE,根据全等三角形的性质可以得到∠1=∠2,AG=AE;因为∠BAD=90°,∠EAF=45°,所以∠2+∠3=45°,从而得到∠1+∠3=45°,于是∠FAG=∠FAE=45°,根据全等三角形判定定理可以得到△FAG≌△FAE,由全等三角形性质可以得到EF=FG=BF+BG=BF+DE;
(2)类比探究:如图②,将Rt△ABC沿斜边翻折得到△ADC,即△ABC≌△ADC,点E,F分别为DC,BC边上的点,且∠EAF=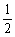∠DAB.求证:EF=DE+BF.

解题思路:类比(1)的思路,添加辅助线为           ,由于△ABC≌△ADC,根据全等三角形性质可以得到AD=AB,由于∠ABC=90°,所以∠ABG=90°,根据全等三角形的判定定理           ,得到           ;由全等三角形的性质可以得到∠BAG=∠DAE,AG=AE;因为∠EAF=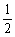∠DAB,所以∠DAE+∠BAF=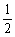∠DAB,等量代换得到∠BAG+∠BAF=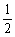∠DAB,于是           ,根据全等三角形的判定定理可以得到           ,又由全等三角形的性质可以得到EF=FG,得到结论DE+BF=EF.
①延长CB到G,使∠GAB=∠DAE,BG=DE,连接AG,②延长CB到G,使BG=DE,连接AG,③SAS,④SSA,⑤△ABG≌△ADE,⑥△FAG≌△FAE,⑦∠EAF=∠GAF,⑧∠CAE=∠CAF;
括号里所填内容的顺序正确的是(    )

• A.②③⑤⑦⑥
• B.①③⑤⑦⑥
  
• C.②④⑥⑦⑤
• D.②③⑤⑦⑧
  

答案

正确答案：A

知识点：三角形全等之类比探究  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>