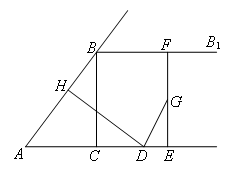
如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB1∥AC．动点D从点A出发沿射线AC方向运动，同时动点E从点C出发沿射线AC方向运动．过点D作DH⊥AB于点H，过点E作EF⊥AC，交射线BB1于点F，G是EF的中点，连接DG．设AD=5a，CE=3a．
（1）当a为何值时，AD=AB，并求出此时DE的长；
（2）当△DEG与△ACB相似时，求a的值．
答案
解：（1）∵∠ACB=90°，AC=3，BC=4
∴AB=5
又∵AD=AB，AD=5a
∴a=1，此时CE=3，
∴DE=AE-AD=3+3-5=1
（2）当点D在点E左侧，即：0≤a<
时，DE=3a+3-5a=3-2a．
若△DEG与△ACB相似，有两种情况：
①△DEG∽△ACB，此时
，即：
，求得：a=
；
②△DEG∽△BCA，此时
，即：
，求得：a=
；
（2）当点D在点E右侧，即：a>时，DE=5a-(3a+3)=2a-3．
若△DEG与△ACB相似，有两种情况：
③△DEG∽△ACB，此时，即：
，求得：a=
；
④△DEG∽△BCA，此时，即：
，求得：a=
．
综上，a的值为或或或．
知识点：相似中的存在性问题
略
略
WORD格式（
