如图，菱形ABCD的边长为20cm，∠ABC=120°．动点P，Q同时从点A出发，其中P以4cm/s的速度，沿A→B→C的路线向点C运动；Q以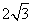
cm/s的速度，沿A→C的路线向点C运动．当P，Q到达终点C时，整个运动随之结束，设运动时间为t（秒）．
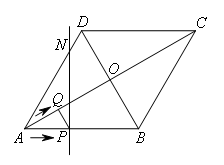
（1）在点P，Q运动过程中，请判断PQ与对角线AC的位置关系，并说明理由．
（2）若点Q关于菱形ABCD的对角线交点O的对称点为M，过点P且垂直于AB的直线l交菱形ABCD的边AD（或CD）于点N．
①当t为何值时，点P，M，N在同一直线上？
②当点P，M，N不在同一直线上时，是否存在这样的t，使得△PMN是以PN为一直角边的直角三角形？若存在，请求出所有符合条件的t值；若不存在，请说明理由．
答案
解：（1）∵AB=20cm，∠ABC=120°
∴∠BAO=30°
∴AO=
cm，AC=
cm
①0<t≤5时，AP=4t，AQ=
t
∴
∵∠BAO=30°
∴△APQ∽△ABO
∴∠AQP=90°
即：PQ⊥AC
②当5＜t≤10时，CP=40－4t，CQ=－t
同理可证：△PCQ∽△BCO
∴∠CQP=90°
即：PQ⊥AC综上，在点P，Q运动过程中，始终有PQ⊥AC．
（2）①由题意得，CM=AQ=t，AP=4t
若点P，M，N在同一直线上，则AM=
t
∴AM＋CM=t＋t=
∴t=
②存在
设l交AC于H
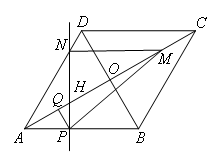
当点N在AD上时，若PN⊥MN，则∠NMH=30°=∠NAH∴MH=2NH，NH=AH
∴AC－CM－AH=2NH=2AH
即：－t－t＝2×t
∴t=2
当点N在CD上时，若PM⊥MN，则∠HMP=30°∴MH=2PH
同理可得：t=
综上，当t=2s或s时，存在以PN为一直角边的直角三角形．
知识点：相似之动点问题
略
略
WORD格式（
