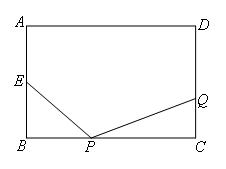
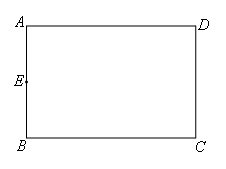
已知：如图，在矩形ABCD中，AB=4cm，BC=6cm，点E为AB中点，如果点P在线段BC上以每秒2cm的速度由点B向点C运动，同时，点Q在线段CD上由点C向点D运动．设点P运动时间为t秒，若某一时刻△BPE与△CQP全等，求此时t的值及点Q的运动速度．
答案
解：如图，由题意得：BP=2t，
∵E为AB中点
∴BE=
∵AB=4cm
∴BE=2cm
∵BC=6cm
∴PC=6-2t
①要使△BPE≌△CPQ，
则需BE=CQ，BP=CP
即CQ=2，2t=6-2t
∴t=
则Q的速度为:VQ=
=
(cm/s)
即当t=，Q的速度是每秒cm时，△BPE≌△CPQ.
②要使△BPE≌△CQP
则需BE=CP,BP=CQ
即2=6-2t，CQ=2t
∴t=2(s)
CQ=4(cm)
则Q的速度为:VQ==2(cm/s)
即当t=2s，Q的速度是每秒2cm时，△BPE≌△CQP.
综上所述：当t=，Q的速度是每秒cm时或者t=2s，Q的速度是每秒2cm时，△BPE和△CPQ全等.
知识点：动点问题
略
略
WORD格式（
