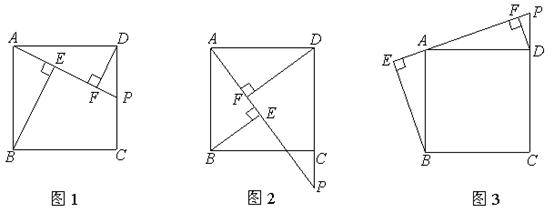
在正方形ABCD中,AB=AD,∠BAD=90°,P是CD边上一点,连接PA,过点B,D作BE⊥PA,DF⊥PA,垂足分别为E,F,如图1.
(1)请探究BE,DF,EF这三条线段有怎样的数量关系?
(2)若点P在DC的延长线上,如图2,那么这三条线段又具有怎样的数量关系?
(3)若点P在CD的延长线上,如图3,那么这三条线段又具有怎样的数量关系?
答案
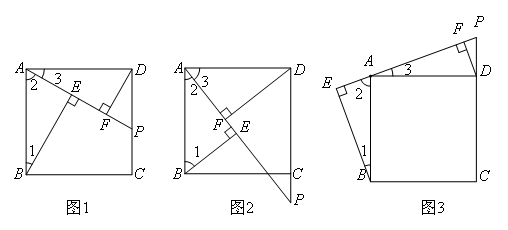
证明:(1)BE=DF+EF,理由如下:
∵BE⊥PA,DF⊥PA
∴∠BEA=∠AFD=90°
∴∠1+∠2=90°
∵∠BAD=90°
∴∠2+∠3=90°
∴∠1=∠3
在△BEA和△AFD中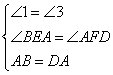
∴△BEA≌△AFD(AAS)
∴BE=AF,AE=DF
∵AF=AE+EF
∴BE=DF+EF
(2)DF=BE+EF,理由如下:
∵BE⊥PA,DF⊥PA
∴∠BEA=∠AFD=90°
∴∠1+∠2=90°
∵∠BAD=90°
∴∠2+∠3=90°
∴∠1=∠3
在△BEA和△AFD中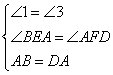
∴△BEA≌△AFD(AAS)
∴BE=AF,AE=DF
∵AE=AF+EF
∴DF=BE+EF
(3)EF=DF+BE,理由如下:
∵BE⊥PA,DF⊥PA
∴∠BEA=∠AFD=90°
∴∠1+∠2=90°
∵∠BAD=90°
∴∠2+∠3=90°
∴∠1=∠3
在△BEA和△AFD中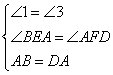
∴△BEA≌△AFD(AAS)
∴BE=AF,AE=DF
∵EF=AE+AF
∴EF=DF+BE
知识点:类比探究
略
略








