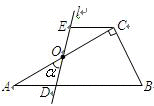
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,点O是AC的中点.过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D.过点C做CE∥AB交直线l于点E,设直线的旋转角为α.
①当四边形EDBC是等腰梯形,α= ( ),AD的长为( );
②当四边形EDBC是直角梯形,α= ( ),AD的长为( );
③当四边形EDBC是菱形,α= ( ). ( )
- A.30°,2;60°,1.5;60°
- B.45°,1;60°,1.5;90°
- C.30°,1;60°,1.5;90°
- D.60°,2;45°,2;60°
答案
正确答案:C
首先应该知道等腰梯形的性质,那就是一组对边平行,另一组对边不平行,但是相等。这时∠BCE=120°,那么△COE≌△AOD,于是有AD=EC,又知∠B=60°,BC=2,则得出线段BD的长度,可求得结果。 (2)为直角梯形,那么ED⊥AB,可知α=60°。与第一题类似, 可得到△COE≌△AOD,O又为AC中点,所以可求得最终结果。 (3)是。理由如下。首先我们应该明白什么是菱形,菱形的性质有哪些。 连接CD,因为∠B=60°,很明显我们可以知道EDBC为一个平行四边形,而且又有△CED和△BCD为正三角形,所以知道两个三角形的便都相等,即四边形EDBC为菱形。证明成立。
略








