已知1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,…
根据上述规律,第100个式子是( )
- A.

- B.
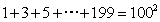
- C.
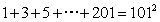
- D.
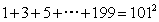
答案
正确答案:C
知识点:探索规律
解答过程:
分析:
标序号,列结构:
①1+3=4=22;
②1+3+5=9=32;
③1+3+5+7=16=42;
④猜测:1+3+5+7+(2×4+1)=52,验证:题干已知1+3+5+7+9=25=52,符合猜测;
…
∴第n个:1+3+5+7+9+…+(2n+1)=(n+1)2
验证:取n=1,1+(2×1+1)=(1+1)2,即1+3=22;
与题干中第一项一致,故第n个式子合理;
当n=100时,代入1+3+5+7+9+…+(2n+1)=(n+1)2得:
1+3+5+7+9+…+(2×100+1)=(100+1)2
即1+3+5+7+9+…+2012=1012
故选C.
(3)易错点:项数对应错误,错误做法如:1+3+5+7+9+…+(2n-1)=(n+1)2
或者1+3+5+7+9+…+(2n+1)=n2.
略







