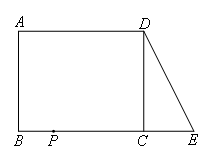
已知:如图,在长方形ABCD中,AB=DC=4,AD=BC=5.延长BC到点E,使CE=2,连接DE.动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒.当t为(    )秒时,△ABP和△DEC全等.

（1）考点：动点问题，全等三角形
（2）解题过程：
解：①当P在BC上时，
由题意得BP=2t
要使△ABP≌△DCE，则需BP=CE
∵CE=2
∴2t=2，t=1
即当t=1时，△ABP≌△DCE
②当P在CD上时，不存在t使△ABP和△DCE全等
③当P在AD上时，由题意得BC+CD+DP=2t
∵BC=5，CD=4，AD=5
∴AP=5+4+5-2t=14-2t
要使△ABP≌△CDE，则需AP=CE
即14-2t=2，t=6
即当t=6时，△ABP≌△CDE．
综上所述，当t=1或t=6时，△ABP和△DEC全等．
故选D

略