如图,在△ABC中,AB=2,AC=4,D是BC的中点,AE平分∠BAC交BC于点E,且DF∥AE.则CF的长为( )
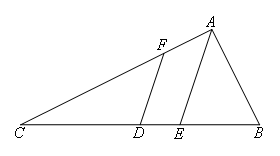
- A.2
- B.
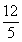
- C.
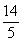
- D.3
答案
正确答案:D
知识点:倍长中线
解:如图,延长FD到G,使得DG=DF,连接BG,延长AE交BG于点H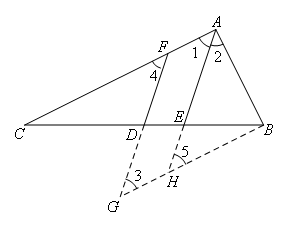
在△CDF和△BDG中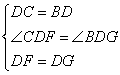
∴△CDF≌△BDG(SAS)
∴CF=BG,∠4=∠3
∴AC∥BG
∵DF∥AE
∴四边形AFGH是平行四边形
∴AF=GH
设AF=x
则GH=x,CF=BG=4-x
∵AE平分∠BAC
∴∠1=∠2
∵AC∥BG
∴∠1=∠5
∴∠2=∠5
∴BH=AB=2
∴GH=BG-BH=2-x
∵AF=GH
∴x=2-x
解得:x=1
∴CF=3
故选D
略








