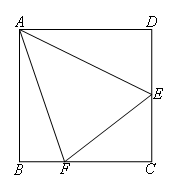
已知:如图,在正方形ABCD中,AD=AB=6,∠D=∠ABC=∠BAD=90°,E,F分别为DC,BC边上的点,且∠EAF=45°,连接EF.若BF=2,DE=3,则EF=( )
- A.3
- B.4
- C.5
- D.6
答案
正确答案:C
知识点:三角形全等之截长补短
解:如图,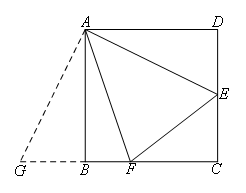
延长CB,在CB的延长线上截取BG=DE,连接AG,
∴∠ABG=∠ABC=∠D=90°
在△ABG和△ADE中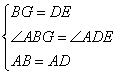
∴△ABG≌△ADE(SAS)
∴AG=AE,∠BAG=∠DAE
∵∠EAF=45°
∴∠DAE+∠BAF=45°
∴∠BAG+∠BAF=45°,
即∠GAF=45°
∴∠GAF=∠EAF
在△AGF和△AEF中,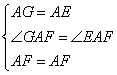
∴△AGF≌△AEF(SAS),
∴EF=GF
∴EF=BG+BF=DE+BF
又∵BF=2,DE=3,
∴EF=5
故选C
略








