如图,将Rt△ABC(其中∠ACB=90°)绕点C顺时针旋转90°得到△DEC,M,N分别为AB,DE的中点,若MN=2,则AB的长为( )
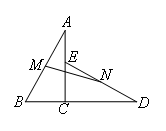
- A.
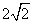
- B.2
- C.

- D.4
答案
正确答案:A
知识点:直角三角形斜边中线等于斜边一半
如图,连接MC,NC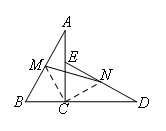
∵旋转是全等变换
∴AB=DE,AC=DC
∵M,N分别是AB,DE的中点
∴![]() ,
,![]()
∴CM=CN
∴△ACM≌△DCN
∴∠ACM=∠DCN
∵∠DCN+∠ECN=90°
∴∠ACM+∠ECN=∠MCN=90°
在Rt△MCN中,MN=2,MC=NC
∴![]()
∴![]() .
.
故选A
略








