在正方形ABCD中,AB=AD,∠BAD=90°,P是CD边上一点,连接PA,过点B,D作BE⊥PA,
DF⊥PA,垂足分别为E,F,如图1.
(3)若点P在CD的延长线上,如图3,请探究此时BE,DF,EF这三条线段满足的数量关系是(    )

1．思路点拨
①对比这道题和前两题的图形，条件和问法，发现基本类似，故可判断这是一道类比探究题，可以照搬前面的思路和做法.
②在本题中，可以直接照搬前面证明三角形全等的方法，用AAS证明△ABE和△DAF全等，从而找到线段之间的关系.
2．解题过程
如图，

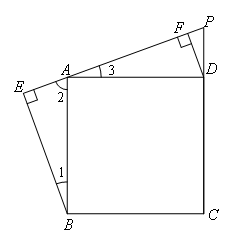
∵∠1+∠2=90°，∠2+∠3=90°
∴∠1=∠3
在△ABE和△DAF中

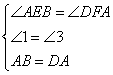
∴△ABE≌△DAF（AAS）
∴AE=DF，BE=AF
∵EF=AE +AF
∴EF=BE +DF
故选B
3．易错点
不能辨识类比探究的类型，每一次都重新想方法，不知道照搬前面的思路和过程.

略