已知:如图,直线CD经过∠BCA的顶点C,点E,F在直线CD上,已知CA=CB,∠BEC=∠CFA=α.
(3)如图3,若0°<∠BCA<90°,若让你添加一个关于∠α与∠BCA的条件,使结论EF=BE-AF仍然成立,则你添加的条件是( )
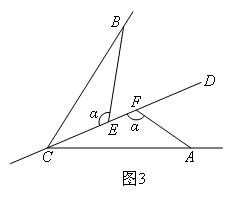
- A.∠BCA=∠α
- B.∠BCA=180°-∠α
- C.∠BCA=2∠α或者∠BCA=∠α
- D.不确定
答案
正确答案:B
知识点:类比探究
1.思路点拨
①辨识类型:对照前两题的图形和结论的问法,可知这是一道类比探究题目.但是对比这三道题的问法,可知应该是条件和结论进行了互换,需要去研究前两题条件背后的本质到底是什么.
②分析结果可知,要想EF=BE-AF,需证明△BCE≌△CAF;
③结合前面两道题可知,当∠α+∠BCA=180°时,可以证明△BCE≌△CAF(AAS),此时结论EF=BE-AF仍然成立.故选B
2.解题过程
如图,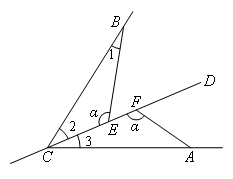
添加∠α+∠BCA=180°之后,
∵∠BCA=∠2+∠3
∠![]() +∠BCA=180°
+∠BCA=180°
∴∠2+∠3+∠![]() =180°
=180°
∵∠1+∠2+∠![]() =180°
=180°
∴∠1=∠3
∴在△BCE和△CAF中
∴△BCE≌△CAF(AAS)
∴BE=CF,CE=AF
∴EF=CF-CE=BE-AF
故选B
略








