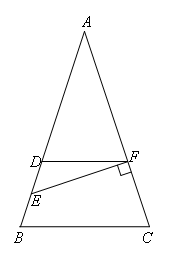
如图,在△ABC中,AB=AC,D是AB上的一点,且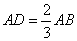,DF∥BC,交AC于点F,E为BD的中点.若EF⊥AC,BC=12,则四边形DBCF的面积为(    )

由DF∥BC，且E是DB中点，容易想到倍长中线．
如图，延长FE交CB的延长于点G，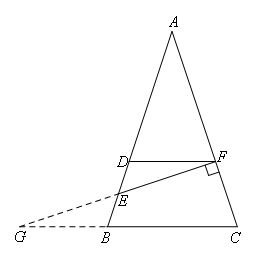

易知△FDE≌△GBE，
∴四边形DBCF的面积转化为△FGC的面积，且此时GB=FD=8，
∴CG=20．
设AD=AF=，则DB=FC=2x，
∴DE=x，则AE=5x．
在Rt△AFE中，则FE=3x，
∴FG=6x．
在Rt△FGC中，FC=2x，FG=6x，CG=20，
由勾股定理可以解得，
∴，，
则△FGC的面积为，
即四边形DBCF的面积为60．

略