如图,⊙O过点B 、C,圆心O在等腰直角△ABC的内部,∠BAC为直角,OA=1,BC=6,则⊙O的半径为( )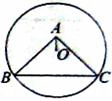
- A.
- B.
- C.
- D.
答案
正确答案:D
延长AO交BC边于点D,再连接OB。由于⊙O过点B 、C,所以线段BC的垂直平分线必过圆心O,又△ABC为等腰直角三角形,BC为斜边,所以BC的垂直平分线必过顶点A,综上可知BC的垂直平分线既过点O又过点A,又由辅助线的做法知AD即为BC边的垂直平分线,D是垂足,所以△OBD为直角三角形。在Rt△OBD中,OB=r,OD=AD-AO=BC-AO=3-1=2,BD=
BC=3,由勾股定理易得r=
,故答案选D
略








