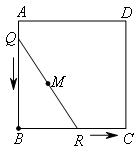
如图，正方形ABCD的边长为2，将长为2的线段QR的两端放在正方形相邻的两边上同时滑动．如果点Q从点A出发，按A→B→C→D→A的方向滑动到A停止，同时点R从点B出发，按B→C→D→A→B的方向滑动到B停止，在这个过程中，线段QR的中点M所经过的路线与正方形围成的图形面积为(    )

首先研究点M在如图所示（点Q在AB上，点R在BC上）的图形上运动的路线．
在线段QR滑动过程中，QR是动点，QR的长度为2不发生变化，M是线段QR的中点不发生变化，并且∠B为直角不发生变化，所以在Rt△QBR中，容易想到斜边中线．
如图所示，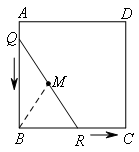

连接BM，
∵M是QR中点，
∴BM=1，
即点M在以点B为圆心，BM长为半径的圆上，并且根据临界状态（QR与AB重合，QR与BC重合）可以判断，运动路径为圆弧，如图所示：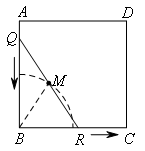

则在QR整个运动过程中，点M的运动路线，如图所示，为4个圆弧．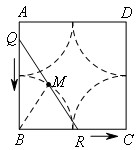

则所经过的路线与正方形围成的图形面积为．

略