如图,抛物线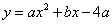 经过C(0,4),D(-3,4)两点,与x轴交于A,B两点(点A在点B右侧).连接BD,点P为抛物线上一点,若∠DBP=45°,则点P的坐标为( )
经过C(0,4),D(-3,4)两点,与x轴交于A,B两点(点A在点B右侧).连接BD,点P为抛物线上一点,若∠DBP=45°,则点P的坐标为( )
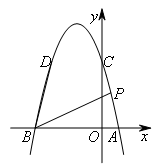
- A.
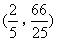
- B.
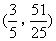
- C.
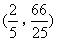 或
或
- D.
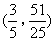 或
或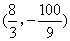
答案
正确答案:A
知识点:二次函数背景下的存在性问题 弦图模型
将C(0,4),D(-3,4)代入,解得![]() ,
,![]() ,
,
∴抛物线的解析式为![]() ,
,
∴B(-4,0),A(1,0).
如图,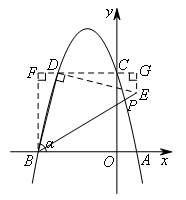
由点D,B的坐标易求得tanα=4,![]() ,
,
要使得∠DBP=45°,点P需在x轴上方的抛物线上.
过点D作BD的垂线,交BP于点E.
通过构造弦图模型来求出点E的坐标,进而表达出直线BE的解析式,通过联立直线BE和抛物线的解析式求出点P的坐标.
如图所示,BF=DG=4,FD=GE=1,
∴E(1,3),
∴直线BE:![]() ,
,
由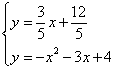 得,
得,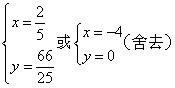 ,
,
∴点P的坐标为![]() .
.
略








