在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A,B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E,F为边OA上的两个动点,且EF=2,则当四边形CDEF的周长最小时,点F的坐标为( )
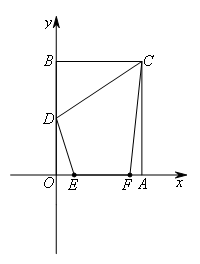
- A.
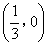
- B.
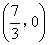
- C.(2,0)
- D.(3,0)
答案
正确答案:B
知识点:轴对称最值问题
通过题意可知,EF和CD的长固定,所以若要四边形CDEF的周长最小,则DE+CF的值最小即可.
如图,CF向左平移两个单位到C′E,此时就转化为要求DE+C′E的最小值.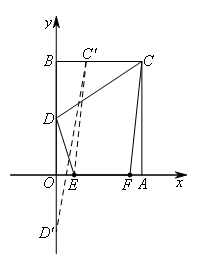
作出点D关于x轴的对称点D′,此时连接C′D′,与x轴的交点即为点E.
根据题意可得,点C′的坐标为(1,4),点D′的坐标为(0,-2),
∴C′D′的直线解析式为:y=6x-2,
∴点E的坐标为![]() ,
,
∴点F的坐标为![]() .
.
故选B
略








