如图,已知抛物线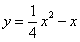 经过原点O和x轴上的一点A,抛物线的顶点为E,对称轴与x轴交于点D.N是坐标平面内任一点,点M从点E出发,沿对称轴向上以每秒1个单位长度的速度匀速运动.设点M的运动时间为t秒,若存在某时刻t,使得以N,A,E,M为顶点的四边形是菱形,则t的值为( )
经过原点O和x轴上的一点A,抛物线的顶点为E,对称轴与x轴交于点D.N是坐标平面内任一点,点M从点E出发,沿对称轴向上以每秒1个单位长度的速度匀速运动.设点M的运动时间为t秒,若存在某时刻t,使得以N,A,E,M为顶点的四边形是菱形,则t的值为( )
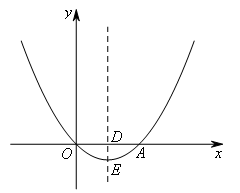
- A.
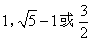
- B.

- C.

- D.
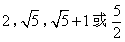
答案
正确答案:B
知识点:菱形的存在性(转等腰)
由抛物线解析式![]() 得,A(4,0),
得,A(4,0),
对称轴为直线x=2,E(2,-1),D(2,0).
∴AD=2,DE=1.
①如图,连接AE,以点A为圆心,AE长为半径作圆,交对称轴于点M(不与点E重合).
此时△AME为等腰三角形,沿底边EM翻折得菱形AMNE.
易得DM=DE=1,
∴EM=2,
∴t=2.
②如图,连接AE,以点E为圆心,AE长为半径作圆,交点E上方的对称轴于点M.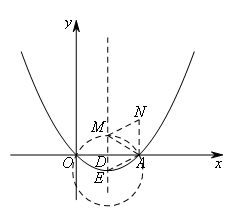
此时△AME为等腰三角形,沿底边AM翻折得菱形ANME.
在Rt△ADE中,由勾股定理得,![]() .
.
易得,![]() ,
,
∴![]() .
.
③如图,作线段AD的垂直平分线,交对称轴于点M.
此时△AME为等腰三角形,沿底边EA翻折得菱形AMEN.
记AE的中点为C,
易得,![]() ,△ADE∽△MCE,
,△ADE∽△MCE,
∴![]() ,即
,即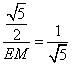 ,
,
∴![]() ,
,
∴![]() .
.
综上得,t的值为![]() .
.
略








