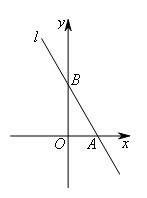
如图,在平面直角坐标系中,直线 与x轴、y轴分别交于点A,B(
与x轴、y轴分别交于点A,B(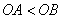 ),
),
且OA,OB的长分别是一元二次方程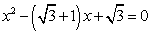 的两个根.P是y轴上的点,Q是坐标平面内的点,若以A,B,P,Q为顶点的四边形是菱形,则点Q的坐标为( )
的两个根.P是y轴上的点,Q是坐标平面内的点,若以A,B,P,Q为顶点的四边形是菱形,则点Q的坐标为( )
- A.
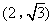 或
或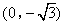
- B.
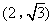 ,
,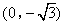 ,(1,2)或(1,-2)
,(1,2)或(1,-2) - C.(-1,0),(1,2),(1,-2)或
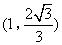
- D.
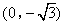 ,
,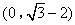 ,
,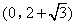 或
或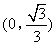
答案
正确答案:C
知识点:菱形的存在性(转等腰)
1.解题要点
①观察题目特征,属于菱形的存在性问题.
②分析定点、动点.菱形的四个顶点中A,B是定点,P,Q是动点,点P在y轴上运动.
③菱形存在性转化为等腰三角形存在性(等腰三角形沿底边翻折可得到菱形).要研究的三角形的三个顶点需条件相对集中,包括定点A,B和y轴上的动点P.
④利用两圆一线确定点P的位置,利用翻折找到对应的点Q的坐标.
2.解题过程
由题意得,![]() ,
,![]() ,
,![]() ,∠OBA=30°,∠OAB=60°.
,∠OBA=30°,∠OAB=60°.
①如图,以A为圆心,AB长为半径作圆,交y轴于点P(与点B不重合).
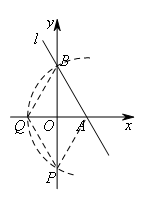
此时△ABP为等腰三角形,沿底边BP翻折得菱形ABQP.
易求得![]() ,Q(-1,0).
,Q(-1,0).
②如图,以B为圆心,AB长为半径作圆,交y轴于点![]() .
.
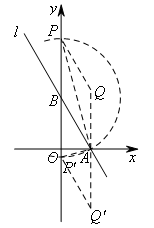
此时![]() 为等腰三角形,沿底边
为等腰三角形,沿底边![]() 翻折可得菱形
翻折可得菱形![]() .
.
∵![]() ∥
∥![]() ,点
,点![]() 在y轴上,
在y轴上,
∴点![]() 的横坐标与点A横坐标相等,均为1.
的横坐标与点A横坐标相等,均为1.
∵![]() ,四边形
,四边形![]() 为菱形,
为菱形,
∴![]() ,
,
即点Q的纵坐标为2,点![]() 纵坐标为-2,
纵坐标为-2,
∴点Q的坐标为(1,2),点![]() 的坐标为(1,-2).
的坐标为(1,-2).
③如图,作线段AB的垂直平分线交y轴于点P.
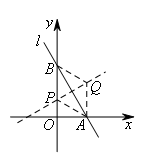
此时△ABP为等腰三角形,沿底边AB翻折得菱形APBQ.
易得∠OBA=∠PAB=∠QAB=30°,![]() ,
,
∴∠OAQ=∠OAB+∠QAB=90°,
∴点Q的坐标为![]() .
.
∴综上得,点Q的坐标为(-1,0),(1,2),(1,-2)或![]() .
.
略








