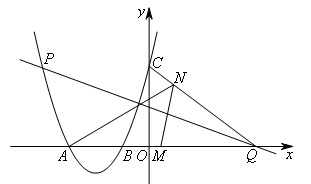
如图，二次函数的图象与x轴交于点A（-3，0）和点B（-1，0），与y轴交于
点C（0，3），P是该图象上的动点．一次函数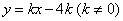
的图象经过点P，且与x轴交于点Q．点M，N分别在线段AQ，CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M，N中有一点到达点Q时，两点同时停止运动，设运动的时间为t秒．
（1）连接AN，当△AMN的面积最大时，t的值为( )
- A.
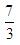
- B.
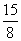
- C.2
- D.
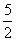
答案
正确答案：A
设抛物线的解析式为y=a（x+3）（x+1），
∵抛物线经过点C（0，3），
∴3=a×3×1，
∴a=1，
∴抛物线的解析式为
．
∵直线PQ的解析式为
，
∴Q（4，0），
∴AQ=7．
在Rt△COQ中，OC=3，OQ=4，
∴CQ=5．
由点M，N的运动可得，AM=3t，MQ=7-3t，CN=t，NQ=5-t，其中
．
如图，过点N作ND⊥x轴于点D．
则ND∥CO，△QND∽△QCO，
∴
，即
，
∴
，
∴
．
略
WORD格式（
