在△ABC中,AB=AC=5,BC=6,点D是BC上的一点,那么点D到AB与AC的距离之和为( )
- A.5
- B.6
- C.4
- D.
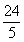
答案
正确答案:D
知识点:等腰三角形的性质
结合题意画出符合题意的图形.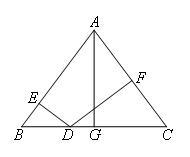
其中,DE⊥AB,DF⊥AC,G为BC的中点,题干所求即DE+DF的值,
根据等面积法可得,DE+DF的值是等腰三角形腰上的高,
∵G为BC中点,AB=AC,
∴CG=BG=3,AG⊥BC,
∵AC=5,
∴AG=4,
设腰上高为h,则![]() ,
,
解得:![]() ,
,
即:点D到AB与AC的距离之和为![]() .
.
故选D
略







