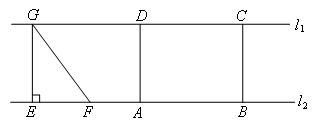
如图,点G,D,C在直线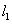 上,点E,F,A,B在直线
上,点E,F,A,B在直线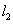 上.若
上.若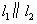 ,四边形ABCD为矩形,Rt△GEF从如图所示的位置出发,沿直线
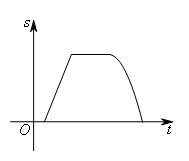
,四边形ABCD为矩形,Rt△GEF从如图所示的位置出发,沿直线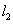 向右匀速运动,直到EG与BC重合,则运动过程中△GEF与矩形ABCD重合部分的面积S随运动时间t变化的图象大致是( )
向右匀速运动,直到EG与BC重合,则运动过程中△GEF与矩形ABCD重合部分的面积S随运动时间t变化的图象大致是( )
- A.
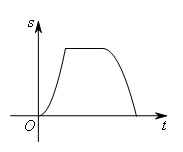
- B.
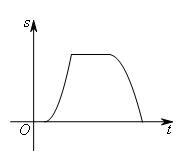
- C.
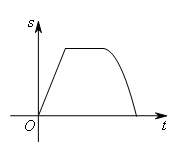
- D.
答案
正确答案:B
知识点:图形运动产生的面积问题 确定函数图象
1.解题要点
①研究图形的运动,根据三角形和矩形的边、顶点的碰撞来确定分段.![]()
②根据几何特征找S与t之间的函数关系.
2.解题过程
①点F到达点A之前无重合部分,S=0.
②点F到达点A之后,EG与AD重合之前,重合部分为△AFH,如图所示,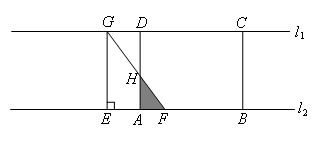
借助图形运动的速度和初始时刻AF之间的距离,可以表达出此时AF的线段长,
再结合∠EFG的正切值可表达出AH的长,
进而得到S与t之间的函数关系式,函数图象为抛物线的一部分,抛物线开口向上.
③当△GEF运动到矩形内部时,重合部分为△GEF,如图所示,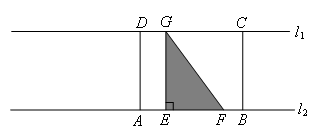
![]() ,为定值.
,为定值.
④点F到达点B之后,重合部分为直角梯形EBMG,如图所示,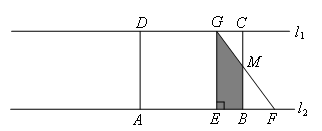
记EG=a,EF=b,设t=0时,BF的长为n,可表达出直角梯形的面积,
得到S关于t之间的函数关系式,函数图象为抛物线,开口向下.
另外可以通过分析得到:
直角梯形的上底BM的长是关于t的一次函数,随t的增大而增大,
下底EG长度不变,
高BE的长是关于t的一次函数,随t的增大而减小.
最后得到S与t之间的函数关系式为二次函数,二次项系数小于0,
由此也可以判断函数关系式的大致图象.
故选B.
略








