在等腰三角形ABC中，已知AB=AC=6，P为BC上一点，且PA=4，则PB·PC的值为(    )

如图，过点A作AD⊥BC于点D．

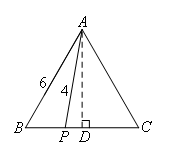
∵△ABC是等腰三角形，
∴BD=CD，
∴PB·PC= (BD-PD)(CD+PD)=BD²-PD²．
在Rt△ABD中，由勾股定理，得BD²=AB²-AD²，
在Rt△APD中，由勾股定理，得PD²=AP²-AD²，
∴BD²-PD²=AB²-AP²=6²-4²=20，
∴PB·PC=20．
故选C．

略