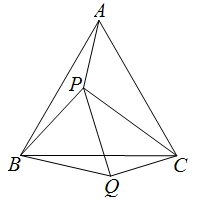
如图，P是等边三角形ABC内的一点，连接PA，PB，PC，以BP为边作∠PBQ=60°，且
BQ=BP，连接PQ，CQ．若PA:PB:PC=3:4:5，则△PQC的形状是( )
- A.等腰三角形
- B.直角三角形
- C.等腰直角三角形
- D.无法确定
答案
正确答案：B
①结合所求目标，条件比较分散，观察到BA=BC且交于点B符合旋转结构特征，则△BQC可看成由△BPA旋转60°得到．
②由△BQC≌△BPA，可得BP=BQ=4k，AP=QC=3k，结合∠PBQ=60°，可得
△BPQ是等边三角形，PQ=4k．
③在△PQC中，PQ=4k，CQ=3k，PC=5k，由勾股定理逆定理可得△PQC为直角三角形．故选B．
略
WORD格式（
